Hranol se skládá ze dvou rovnoběžných podstav a pláště. Kalkulačka provádí výpočty v kolmém pravidelném hranolu. Kolmý hranol má boční strany kolmé na podstavy. Pravidelný čtyřboký hranol.

Kvádr je trojrozměrné těleso – rovnoběžnostěn, jehož stěny tvoří šest pravoúhlých čtyřúhelníků (zpravidla obdélníků, ale existují i speciální případy jako např. čtverec). Má tři skupiny rovnoběžných hran shodné délky (v rámci skupiny).

Tyto délky jsou obvykle označovány jako délka, šířka a výška kvádru. Předpokládané znalosti: hranol s podstavou lichoběžníku, Pythagorova věta. Podle Pythagorovy věty vypočítáme výšku . Vypočítejte povrch a objem hranolu.

Komentované řešení příkladu na objem a povrch pravidelného čtyřbokého hranolu. Trojboký hranol (n = 3) Čtyřboký hranol (n = 4). Zdroj: Dana Rosiarová Pětiboký hranol (n = 5).

Kolmé hranoly mají boční hrany navzájem rovnoběžné.

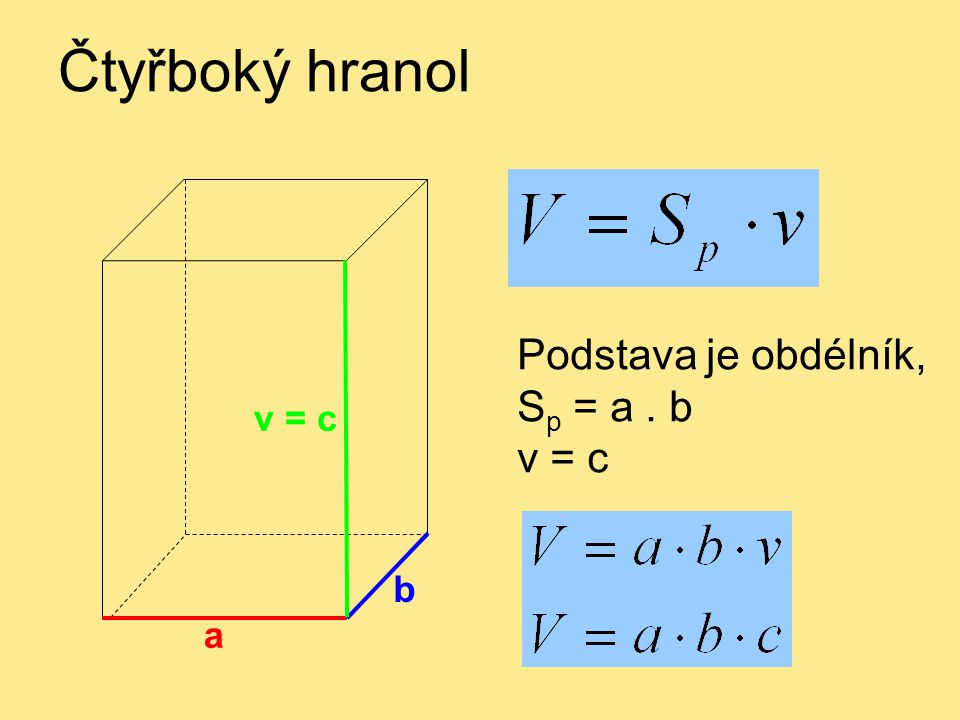
Na obrázku je čtyřboký kolmý hranol ABCDEFGH. Dobrý den, poradit z ranolem. Spl,S,V S je obsah V objem ale Spl? Lze vypočítat jeho objem a povrch. Objem_a_povrch_kvadru_a_.

Teoretická časť Hranol je priestorový geometrický útvar, pozostávajúci z dvoch podstáv a plášťa. Rozlišujeme základné typy hranolov podľa niekoľkých vlastností: 1. Kosý hranol má medzi stenou a postavou . Spielwarenmesse v Německu. Vaše objednávky vyřídíme po našem návratu. Prosím, použijte minimálně znaky!

VZORCE – POVRCH A OBJEM KOLMÉHO HRANOLU. Provozuje Národní ústav pro vzdělávání, školské poradenské zařízení pro další vzdělávání pedagogických pracovníků (NÚV). Název DUTělesa – čtyřboký hranol.

Vzdělávací předmět: Matematika. Tematická oblast: Matematika a její . Sestrojte jeho řez danou rovinou α. Popis konstrukce : V náryse se všechny hrany zobrazí do bodu, proto postupujeme obdobně jako u příkladu 1.

Stereometrie se zabývá útvary, které nelze umístit do roviny. Mezi tyto útvary patří například hranol , krychle, kužel, jehlan a další. Slovo stereometrie je řeckého původu a jeho.

Narýsujeme pravidelný čtyřboký jehlan ABCDV. Ta má tvar čtverce, proto budeme opět postupovat podobně jako při rýsování . Z okna slyšel slova učitele: „Jaký povrch může mít pravidelný čtyřboký hranol , víte -li, že délky všech jeho hran jsou v centimetrech vyjádřeny celými čísly a že jeho objem je. Toto důležité číslo pan Vlk neslyšel, protože zrovna projelo okolo auto. Za chvíli slyšel žáka hlásícího výsledek 9cm2.

Učitel na to řekl: „Ano, ale. Kolik bočních stěn má čtyřboký hranol ? Celkový počet bočních stěn je tedy 4.